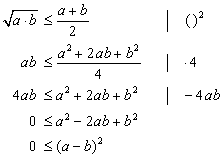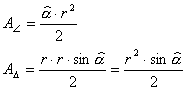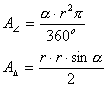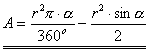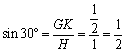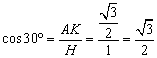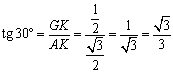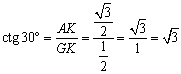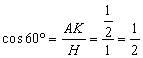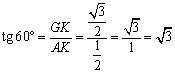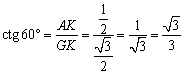1.Der größte gemeinsame Teiler

(ggT)

Definition: Der größte gemeinsame Teiler von zwei oder mehreren Zahlen ist die größtmögliche Zahl, die Teiler von allen gegebenen Zahlen ist.

Bezeichnung:

Man bestimmt den größten gemeinsamen Teiler mehrerer Zahlen, indem man diese zunächst in Primfaktoren zerlegt und danach bildet das Produkt der gemeinsamen Primfaktoren mit dem kleinsten Exponenten.

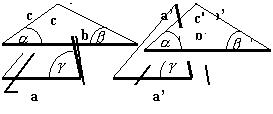
z.B.

210	2
105	3
35	5
7	7
1

340	2
170	2
85	5
17	17
1

2.Das kleinste gemeinsame Vielfache

[kgV]

Definition: Das kleinste gemeinsame Vielfache von zwei oder mehreren Zahlen ist die kleinstmögliche Zahl, die Vielfache von allen gegebenen Zahlen ist.

Bezeichnung:

Man bestimmt das kleinste gemeinsame Vielfache mehrerer Zahlen, indem man diese zunächst in Primfaktoren zerlegt und danach bildet das Produkt aller vorkommenden Faktoren mit dem höchsten Exponenten.

60 | 2

30 | 2

15 | 3

5 | 5

1 |

24 | 2

12 | 2

6 | 2

3 | 3

1 |

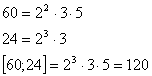
z.B. :

3.Was sind die Primzahlen? Wann sagt man, dass zwei oder mehrere Zahlen relativ prim sind?

a, Primzahlen:

Definition: Diejenigen natürlichen Zahlen, die genau zwei Teiler haben (1 und sich selbst), nennt man Primzahlen. Die Zahl 1 ist keine Primzahl.

z.B.: 2;3;5;7;11;13;17;19;23;29...

b, Relativ Primzahlen:

Definition: Ist der größte gemeinsame Teiler von zwei positiven ganzen Zahlen gleich 1, so sagt man, dass diese Zahlen teilerfremd oder relativ prim sind.

= 1 Þ a und b sind relativ prim

z.B.: (5;11) = 1 5 und 11 sind relativ prim

(8;9) = 1 8 und 9 sind relativ prim

4.Was bedeutet, dass die Addition und die Multiplikation von reellen Zahlen kommutativ, assoziativ und distributiv ist?

a, Addition: Die Addition von reellen Zahlen ist kommutativ und assoziativ:

- kommutativ (vertauschbar)

Bei der Addition von zwei Zahlen darf man die Reihenfolge der beiden Zahlen vertauschen, ihre Summe bleibt dabei unverändert.

- assoziativ (anders verbindbar)

Werden mehrere Zahlen addiert, so darf man die Zahlen auf beliebige Weise gruppieren.

b, Multiplikation: kommutativ, assoziativ, distributiv

- kommutativ:

Bei der Multiplikation von zwei Zahlen darf man die Reihenfolge der Zahlen vertauschen, ihr Produkt bleibt unverändert.

- assoziativ:

Werden mehrere Zahlen miteinander multipliziert, so darf man dabei die Zahlen auf beliebige Weise gruppieren.

- distributiv: (verteilbar)

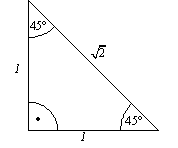
Wird eine Summe von reellen Zahlen mit einer reellen Zahl multipliziert, so ist das Ergebnis gleich der Summe der Produkte aus den einzelnen Summanden und dieser reellen Zahl.

5.Definieren Sie den Begriff der direkten Proportionalität und der umgekehrten/indirekten Proportionalität!

a, Eine Zuordnung wird direkt proportional genannt, wenn der Quotient der zusammengehörenden Paare konstant ist.

konstant y ~ x

x: Anzahl der Blumen	1	2	3	4	5	6	7
y: Preis (Ft)	150	300	450	600	750	900	1050

Der Graph der direkten Proportionalität ist eine Ursprungsgerade.

y

x

b, Eine Zuordnung wird indirekt/umgekehrt proportional genannt, wenn das Produkt der zusammengehörenden Paare konstant ist..

konstant

x: Anzahl der Teilnehmer	1	2	4	8	10
y: Fahrkosten pro Kopf (Ft)	8000	4000	2000	1000	800

Der Graph der umgekehrten/indirekten Proportionalität ist eine Hyperbel.

y

x

6.Wie definiert man die Potenz einer reellen Zahl a mit einem positiven ganzzahligen Exponenten?

Eine reelle Zahl a wird mit n potenziert, wenn sie n-mal mit sich selbst multipliziert wird.

heißt Potenz

a ist die Basis

n ist der Exponent

ist ein Produkt aus n Faktoren, wobei alle Faktoren a sind

7.Beweisen Sie die folgenden Identitäten (a und b sind reelle Zahlen, k und n sind positive natürliche Zahlen)!

a,

Aus der Definition der Potenzen (eine reelle Zahl a wird mit n potenziert, wenn sie n-mal mit sich selbst multipliziert wird) und aus der kommutativen und assoziativen Eigenschaft der Multiplikation folgt, dass man ein Produkt faktorenweise potenzieren kann.

b,

Aus der Definition der Potenzen und aus der Regel, wie man Brüche miteinander multipliziert (Zähler mit Zähler, Nenner mit Nenner) folgt, dass man einen Bruch potenzieren kann, indem man den Zähler und den Nenner potenziert.

c,

Man potenziert Potenzen, indem man die Basis übernimmt und die Exponenten multipliziert.

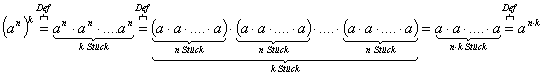
8.Definieren Sie die Quadratwurzel einer nichtnegativen reellen Zahl! Was ergibt?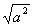

Die Quadratwurzel aus einer nichtnegativen Zahl a ist eine solche nichtnegative Zahl, deren Quadrat gleich a ist.

In Formeln:

,da und

z.B.:; da und

nicht definiert

9. Was versteht man unter rationale Zahlen?

Rationale Zahlen (Q) sind alle Zahlen von der Form , wobei a und b ganze Zahlen sind und ist.

z.B.: ; ;

Rationale Zahlen in Form eines Dezimalbruches können endlich oder unendlich periodisch sein.

10.Was besagt der Fundamentalsatz der Zahlentheorie?

Jede zusammengesetzte Zahl lässt sich von der Reihenfolge abgesehen eindeutig als ein Produkt von Primzahlen aufschreiben.

z.B.:

72	3
24	3
8	2
4	2
2	2
1

72	2
36	3
12	2
6	3
2	2
1

11. Beweisen Sie, dass 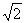eine irrationale Zahl ist!

ist irrational, wenn man sie nicht als Quotient von zwei ganzen Zahlen aufschreiben kann.

Beweis (indirekt):

Annahme: ist eine rationale Zahl, sie lässt sich in der Form darstellen.

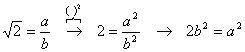
ist eine gerade Zahl Þ muss ebenfalls eine gerade Zahl sein, das ist aber nur dann der Fall, wenn a selber eine gerade Zahl ist, das heißt: , wobei

Damit

ist auch eine gerade Zahl Þ b muss auch eine gerade Zahl sein. So müssen a und b gleichzeitig gerade Zahlen sein, dann können sie nicht teilerfremd sein Þ Widerspruch zur Annahme Þ ist keine rationale Zahl

12. Wie definiert man die Potenz einer positiven Zahl, wenn der Exponent...

a, Null ist?

b, eine negative ganze Zahl ist?

c, eine rationale Zahl ist?

, ,

13. Was versteht man unter der n-ten Wurzel einer reellen Zahl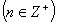? Geben Sie den Wert vo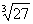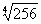n; ;an!

a, Wenn der Wurzelexponent n eine gerade Zahl ist:

Die n-te Wurzel aus einer nichtnegativen Zahl a ist eine solche nichtnegative Zahl, deren n-te Potenz gleich a ist.

b, Wenn der Wurzelexponent n eine ungerade Zahl ist:

Die n-te Wurzel aus einer (reellen) Zahl a ist eine solche Zahl, deren n-te Potenz a ist.

, weil

, weil und,

, weil

14. Beweisen Sie die folgenden Identitäten!

a, , falls n gerade ist:

falls n ungerade ist:

Da alle beide Seiten nichtnegativ sind, ist die Potenzierung der Ausdrücke eine äquivalente Umformung:

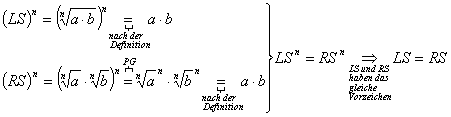
b, 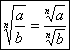, sonst a und b wie oben

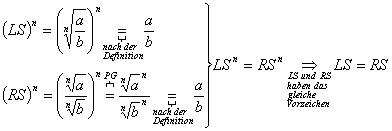
c,

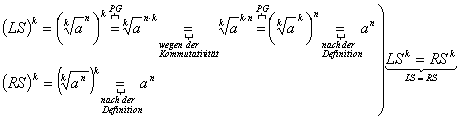
Erklärung der Abkürzungen:

LS = linke Seite

RS = rechte Seite

PG = Potenzgesetz

15. Was versteht man unter Normalform einer reellen Zahl? Schreiben Sie die Normalform der folgenden Zahlen auf! 0.000173;58200000;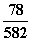

Die Normalform einer reellen Zahl:

, wobei eine Zahl zwischen 1 und ,

und k eine ganze Zahl ist.

k – Charakteristik (sie gibt die Größenordnung der Zahl an)

Jede Zahl kann in Normalform geschrieben werden.

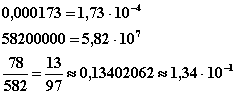
16. Was bedeutet ?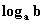

Unter dem Logarithmus einer positiven Zahl b zur Basis a versteht man den Exponenten, mit dem a potenziert b ergibt.

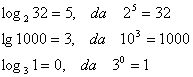
Bemerkungen:

17. Die Logarithmengesetze

Nach der Definition des Logarithmus können wir folgende Zusammenhänge aufschreiben und bei den einzelnen Beweispunkten verwenden (*).

Für a,b,c gelten folgende:

a, Der Logarithmus eines Produktes

I. nach der Definition des Logarithmus II. mit der Anwendung des Potenzgesetzes Aus I und II

Die Exponentialfunktion ist streng monoton. Die Basen sind gleich (aber ungleich 1) Þ Die Exponenten müssen auch gleich sein.

ß

Der Logarithmus eines Produktes ist gleich der Summe der Logarithmen der Faktoren.

b, Der Logarithmus eines Quotienten

I. nach der Definition des Logarithmus

II. mit Hilfe des Potenzgesetzes:

Aus I und II

ß Die Exponentialfunktion ist streng monoton.

Der Logarithmus eines Quotienten ist gleich der Differenz aus dem Logarithmus des Dividenden und dem Logarithmus des Divisors.

c, Der Logarithmus einer Potenz

I. nach der Definition des Logarithmus

II. mit Hilfe des Potenzgesetzes:

Aus I und II

ß Die Exponentialfunktion ist streng monoton.

Der Logarithmus einer Potenz ist gleich dem Produkt aus dem Logarithmus der Potenzbasis und dem Potenzexponenten.

20. Lösungsformel der quadratischen Gleichung

_, ist die allgemeine, auf Null reduzierte Form der Gleichung zweiten Grades.

Wir führen äquivalente Umformungen durch:

a ausklammern

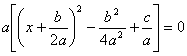quadratisches Ergänzen

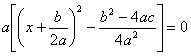gemeinsamer Nenner

falls ,(gilt immer)

(heißt Diskriminante)

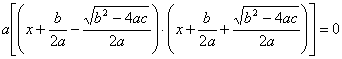III. binomische Formel

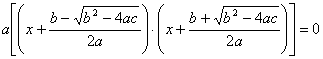gemeinsamer Nenner

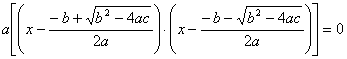
Ein Produkt ist Null, wenn einer der Faktor Null ist:

21. Die Diskriminante

Sie kommt in der Lösungsformel der Gleichung zweiten Grades vor.

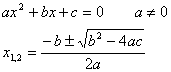Diskriminante: was unter der Wurzel steht

Um die Gleichung lösen zu können, muss gelten:

Die Diskriminante entscheidet über die Anzahl der Lösungen:

D>0

Es gibt zwei verschiedene Lösungen.

D=0

Es gibt eine (zwei gleiche| zusammenfallende) Lösung(en).

D<0

Es gibt keine reelle Lösung.

22. Zusammenhang zwischen den Wurzeln und den Koeffizienten der quadratischen Gleichung (Die Formeln von Vieta)

I. Methode:

Normalform der Gleichung zweiten Grades Produktform der Gleichung zweiten Grades

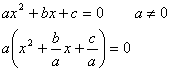
Die Koeffizienten des linearen Gliedes müssen gleich sein.

Die konstanten Glieder müssen auch gleich sein.

II. Methode:

Die quadratische Gleichung:

besitzt die Lösungen , wobei gelten muss.

23. Das arithmetische und das geometrische Mittel zweier nichtnegativen Zahlen

Das arithmetische Mittel:

Unter dem arithmetischen Mittel zweier nicht negativen reellen Zahlen versteht man die Hälfte der Summe der angegebenen Zahlen.

Das geometrische Mittel:

Unter dem geometrischen Mittel zweier nicht negativen reellen Zahlen versteht man die Wurzel aus dem Produkt der angegebenen Zahlen.

Das arithmetische Mittel ist immer größer oder gleich dem geometrischen Mittel.

/Gleichheit besteht, wenn die zwei Zahlen gleich sind./

Beispiel:

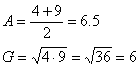
24. Was bedeutet…

a, der Abstand eines Punktes von einer Geraden;

b, der Abstand zweier parallelen Geraden;

c, der Abstand eines Punktes von einer Ebene;

d, der Abstand von zwei parallelen Ebenen ?

a, Der Abstand eines Punktes von einer Geraden: aus dem Punkt wird auf die Gerade ein Lot gefällt, der Abstand ist die Länge der Strecke zwischen dem Punkt und der Geraden.

Abstand ist 0

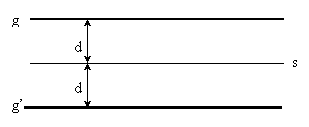
b, Der Abstand zweier parallelen Geraden: aus irgendwelchem Punkt der ersten Geraden wird auf die andere Gerade das Lot gefällt, der Abstand ist die Länge der Strecke des Lotes zwischen den beiden Geraden.

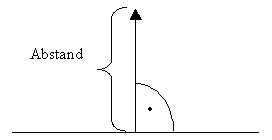
c, Unter dem Abstand eines Punktes von der Ebene versteht man die Länge des Lotes aus dem Punkt auf die Ebene.

.

E

Abstand

P

Abstand ist 0

.P

d, Der Abstand zweier paralleler Ebenen: aus einem beliebigen Punkt der einen Ebene wird auf die andere Ebene das Lot gefällt. Die Länge dieses Lotes ist der Abstand.

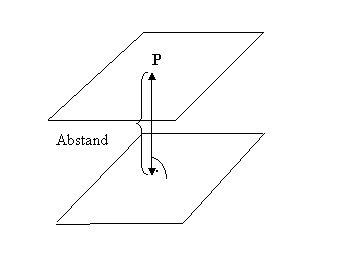
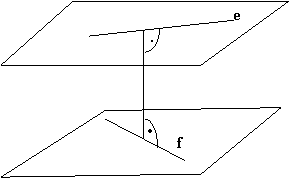
25. Was versteht man unter dem Abstand zweier windschiefen Geraden?

Definition: Zwei Geraden sind windschief, wenn sie keinen gemeinsamen Punkt haben, aber auch nicht parallel sind. Die windschiefen Geraden liegen nicht in derselben Ebene.

Es gibt nur eine Gerade, die beiden windschiefen Geraden senkrecht schneidet. Diese Gerade nennt man die normale Transversale (Orthogonale) der beiden windschiefen Geraden.

Wenn man durch jede windschiefe Gerade eine zur anderen Gerade parallele Ebene legt, dann ist der so entstandene Abstand der zwei Ebenen gleich dem Abstand der zwei windschiefen Geraden.

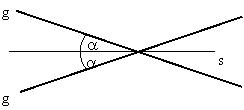
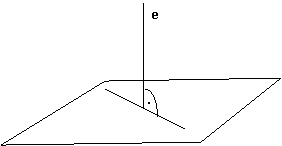
26. Was bedeutet der Neigungswinkel...

a, einer Geraden mit einer Ebene?

b, zweier Ebenen?

Voraussetzungen:

I. Unter dem Neigungswinkel zweier Geraden versteht man den kleineren eingeschlossenen Winkel.

II. Wenn die Geraden senkrecht aufeinander stehen, dann ist der Neigungswinkel 90°.

III. Die gefragten Neigungswinkel kann man auf diese Definition zurückführen.

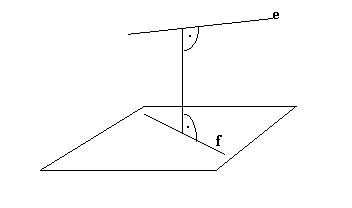
a, Wenn die Gerade senkrecht auf die Ebene steht, also senkrecht auf alle solche Geraden der Ebene, die durch den Schnittpunkt der Geraden und der Ebene verlaufen, dann ist der Neigungswinkel 90°.

Wenn die Gerade parallel zu der Ebene ist, dann ist der Neigungswinkel 0°.

.

.

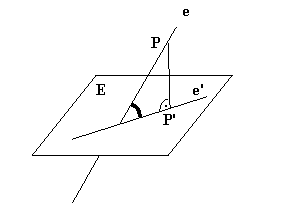
e

Die Gerade e wird senkrecht auf die Ebene projektiert: e’.

Der Neigungswinkel der Geraden mit der Ebene wird der Winkel zwischen der Geraden e und der projizierten Geraden e’.

Wenn die Gerade die Ebene schneidet, aber steht nicht senkrecht darauf:

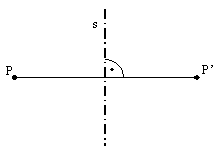
b, Wenn die zwei Ebenen parallel sind, dann ist der Neigungswinkel 0°.

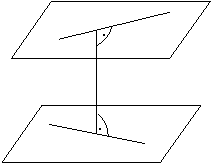
Wenn die zwei Ebenen nicht parallel sind, dann besitzen sie eine gemeinsame Schnittgerade s. In einem beliebigen Punkt P der Schnittgeraden errichtet man die Senkrechten k und l auf der Schnittgeraden in beiden Ebenen.

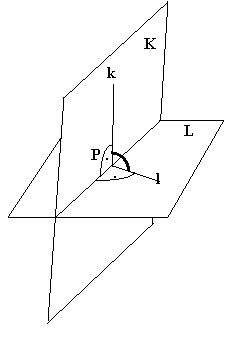
Der Neigungswinkel der Ebenen ist der Neigungswinkel dieser zwei Senkrechten (k und l).

Der Neigungswinkel ist unabhängig von der Wahl des Punktes P.

27. Was bedeutet der Neigungswinkel zweier windschiefen Geraden?

Definition: Zwei Geraden sind windschief, wenn sie keinen gemeinsamen Punkt haben, aber auch nicht parallel sind. Sie liegen nicht in derselben Ebene.

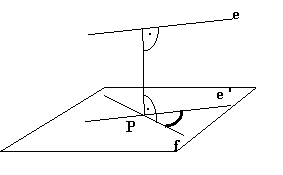Man konstruiert die Gerade e’, die durch einen beliebigen Punkt P der Geraden f verläuft und zu der gegebenen Gerade e parallel ist. Der Neigungswinkel zweier windschiefen Geraden ist der Neigungswinkel der Geraden e’ und f.

Der Neigungswinkel ist unabhängig von der Wahl des Punktes P.

28. Wann nennt man zwei Figuren deckungsgleich?
Zählen Sie die Grundfälle der Kongruenz von Dreiecken auf!

Definition: Zwei Figuren sind kongruent, wenn es solche Kongruenzabbildung gibt, welche die eine Figur in die andere Figur überführt.

Kongruente Transformationen:

I. Achsenspiegelung

II. Punktspiegelung

III. Drehung

IV. Verschiebung

V. alle Verkettungen von dieser Abbildungen

Das Zeichen der Kongruenz:

Die Grundfälle der Kongruenz von Dreiecken:

Zwei Dreiecke sind kongruent, wenn

I. – die entsprechenden Seiten des Dreiecks gleich
lang sind (SSS)

II. – zwei – zwei Seiten und der von ihnen
eingeschlossene Winkel gleich sind(SWS)

III. – zwei – zwei Seiten und der längeren Seite
gegenüber liegende Winkel gleich sind (SSW_gr.)

IV. – eine Seite und die anliegenden Winkel gleich
sind (WSW)

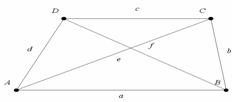
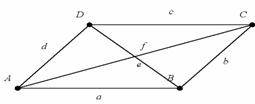
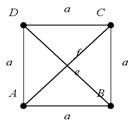
29. Kategorisieren Sie bitte die Vierecke

a, nach der Anzahl der parallelen Seiten

b, nach der Gleichheit der Seiten

Jedes Viereck hat: - 4 Seiten (a,b,c,d)

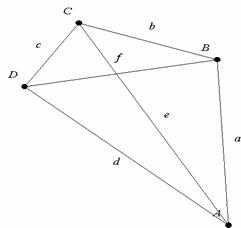
- 4 Eckpunkte (A,B,C,D)

- 4 Winkel

- 2 Diagonalen (e,f)

a, Aufteilung nach der Anzahl der parallelen Seiten

1. – Trapez: hat ein paralleles Seitenpaar

2. – Parallelogramm: hat zwei parallele Seitenpaare.

Jedes Parallelogramm ist gleichzeitig ein Trapez

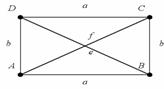
AB||CD AB=CD

BC||AD BC=AD

Spezielle Parallelogramme: - Quadrat

-Rechteck

-Rhombus(= die Raute)

Bemerkung:

Quadrat:

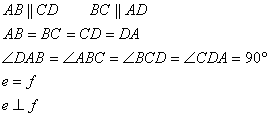
Rechteck:

Rhombus:

b, Aufteilung nach der Gleichheit der Seiten

1. Zwei – zwei gegenüberliegende Seiten sind gleich:

Parallelogramm

Spez.: Rhombus

Rechteck

Quadrat

2. Zwei – zwei benachbarte Seiten sind gleich

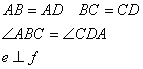
Deltoid

Spez.: Rhombus

Quadrat

3. Alle Seiten sind gleich

Rhombus

Spez.: Quadrat

30. Welches Viereck wird Sehnenviereck oder Tangentenviereck genannt?

SEHNENVIERECK: ein Viereck, dessen Seiten Sehnen eines Kreises sind, nennt man Sehnenviereck.

Die Beziehung zwischen den Winkeln
eines Sehnenvierecks:

Satz: In jedem Sehnenviereck beträgt die Summe
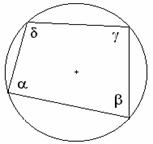
der gegenüberliegenden Winkeln 180°.

Kehrsatz: Ist in einem Viereck die Summe der gegenüberliegenden Winkel 180°, so ist das Viereck ein Sehnenviereck.

Spezielle Sehnenvierecke:

-Quadrat, Rechteck, symmetrisches Trapez

D

G

H C

O

F

A E B

TANGENTENVIERECK: ein Viereck, dessen Seiten
Tangenten eines Kreises sind, nennt man
Tangentenviereck.

Die Beziehung zwischen den Seiten
eines Tangentenvierecks:

Satz: In jedem Tangentenviereck sind die Summen
der gegenüberliegenden Seiten gleich.

AB+CD=BC+DA

Kehrsatz: Sind in einem Viereck die Summen der gegenüberliegenden Seiten gleich, so ist das Viereck ein Tangentenviereck.

Spezielle Tangentenvierecke:

-Quadrat, Rhombus, Deltoid

31. Was nennt man Mittellinie?

a, bei einem Parallelogramm

b, bei einem Trapez

c, bei einem Dreieck

Berechnen Sie die Länge der Mittellinie, wenn die Seitenlängen gegeben sind!

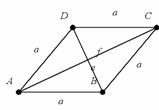
a, Die Mittellinie eines Parallelogramms:

Definition: Die Mittellinie eines Parallelogramms ist die Verbindungsstrecke der Mittelpunkte der zwei gegenüberliegenden parallelen Seiten. (Jedes Parallelogramm hat zwei Mittellinien)

E; F; G; H – Halbierungspunkte

EG; FH – Mittellinie

D G C

H F

A E B

Satz:

Die Mittellinie verläuft parallel zu den nicht halbierten Seiten des Parallelogramms. Sie ist genau so lang, wie die zwei parallelen Seiten des Parallelogramms.

EG||BC||AD und EG=BC=AD

HF||AB||CD und HF=AB=CD

Beweis:

H und F sind Mittelpunkte der Seiten AD und BC Þ AH =BF

Gleichzeitig sind AH und BF parallel Þ ABFH ist ein Parallelogramm ÞAB||HF und AB=HF

Analog kann man der Beweis für die Mittellinie EG führen.

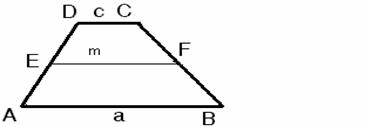
b, Die Mittellinie eines Trapezes:

Definition: Die Mittellinie eines Trapezes ist die Verbindungsstrecke der Mittelpunkte der beiden Schenkel.

E;F – Halbierungspunkte

EF – Mittellinie

Satz:

Die Mittellinie eines Trapezes verläuft parallel zu den zwei parallel liegenden Seiten des Trapezes (zu den Basen). Ihre Länge ist gleich dem arithmetischen Mittel der Basenlängen.

EF||AB||CD und

Beweis:

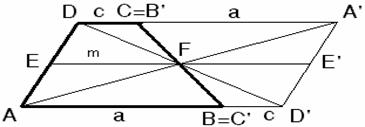
Das Trapez wird an F gespiegelt. Nach den Eigenschaften der Spiegelung ist das Viereck AD’A’D ein Parallelogramm mit der Seitenlänge a + c. EE’ ist die Mittellinie des Parallelogramms AD’A’D Þ EE’ = AD’ und

c, Die Mittellinie eines Dreiecks:

Definition: Die Mittellinie eines Dreiecks ist die Verbindungsstrecke der Mittelpunkte zweier Seiten eines Dreiecks. Jedes Dreieck hat drei Mittellinien.

D; E; F –Halbierungspunkte

DE; EF; FD – Mittellinien

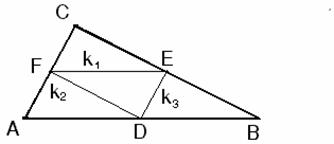
Satz:

Die Mittellinie des Dreiecks verläuft parallel zu der nicht halbierten Seite, ihre Länge ist gleich der Hälfte der nicht halbierten Seite.

Beweis:

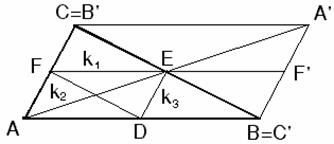
Das Dreieck wird an E gespiegelt: Parallelogramm ABA’C. FF’ ist Mittellinie des Parallelogramms. Þ FF’=AB und FF’||AB

2 EF=AB und EF||AB

Analog kann man den Beweis für DE und FD führen.

33.

a.) Geben Sie die Menge aller Punkte einer Ebene (des Raumes) an, die gleich weit von zwei gegebenen Punkten entfernt sind.

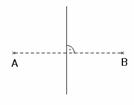
Die Menge aller Punkte der Ebene, die gleich weit von zwei gegebenen Punkten A und B entfernt sind, ist die Mittelsenkrechte der Strecke, die diese Punkte verbindet.

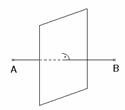
Die Menge aller Punkte des Raumes, die gleich weit von zwei gegebenen Punkten A und B entfernt sind, ist die Ebene, die senkrecht auf der Geraden AB steht und durch die Mitte der Strecke AB geht (die mittelsenkrechte Ebene).

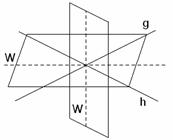
b, Geben Sie die Menge aller Punkte der Ebene (des Raumes) an, die gleich weit von zwei gegebenen Geraden entfernt sind.

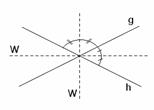
Die Menge aller Punkte der Ebene, die gleich weit von zwei gegebenen Geraden g und h entfernt sind, bildet die Winkelhalbierende W und W’ der Winkel.

Anmerkung:

Sind die zwei Geraden parallel, so ist die gesuchte Punktmenge die Mittelparallele die beiden Geraden.

Die Menge aller Punkte des Raumes, die gleich weit von zwei gegebenen Geraden g und h entfernt sind, besteht aus zwei Ebenen, die durch den Schnittpunkt der beiden Geraden gehen und mit den beiden Geraden gleich große Winkel bilden (die Winkelhalbierenden Ebenen).

Anmerkung:

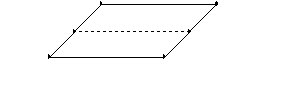Sind die Geraden parallel, so ist die gesuchte Punktmenge eine Ebene, die parallel zu den beiden Geraden ist, den Abstand der Geraden halbiert und senkrecht zu der von g und h bestimmten Ebene ist(die mittelparallele Ebene).

34. Bestimmen Sie

a, die Menge aller Punkte der Ebene (des Raumes), die gleich weit von drei gegebenen Punkten entfernt sind.

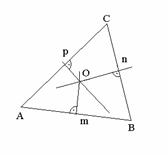
Die Menge aller Punkte der Ebene, die gleich weit von drei gegebenen - nicht kollinearen - Punkten (A, B und C) entfernt sind, hat ein einziges Element: den Mittelpunkt des Umkreises des durch die drei Punkte bestimmten Dreiecks.

Anmerkung:

Sind die Punkte kollinear, so ist die gesuchte Punktmenge:.

Die Menge aller Punkte des Raumes, die gleich weit von drei gegebenen, nicht kollinearen Punkten (A, B und C) entfernt sind, ist eine Gerade, die senkrecht auf der Ebene (die durch diese Punkte bestimmt ist) steht und durch den Umkreismittelpunkt des Dreiecks ABC geht.

Anmerkung:

Sind diese Punkte kollinear, so ist die gesuchte Punktmenge: .

b, die Menge aller Punkte einer Ebene, die von drei gegebenen Geraden der Ebene gleich weit entfernt sind.

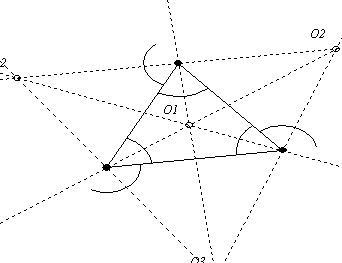
Die Menge aller Punkte einer Ebene, die von drei gegebenen, paarweise nicht parallelen Geraden (g, h und i) der Ebene gleich weit entfernt sind, besteht aus 4 Punkten, dem Inkreismittelpunkt und den drei Ankreismittelpunkten des Dreiecks, das durch die drei Geraden bestimmt ist.

Anmerkungen:

Sind zwei von den Geraden parallel, so besteht die gesuchte Punktmenge aus zwei Punkten: den Schnittpunkten der Mittelparallelen von g und h mit den Winkelhalbierenden der Winkel Ð(g; i) bzw. Ð(h; i).

Sind alle drei Geraden parallel, so ist die gesuchte Punktmenge: .

35. Beweisen Sie:

In einem Dreieck schneiden sich die Mittelsenkrechten der Seiten in einem Punkt, dieser Punkt ist der Mittelpunkt des Umkreises.

Beweis:

Es seien m, n und p die Mittelsenkrechten der Seiten AB, BC , CA.

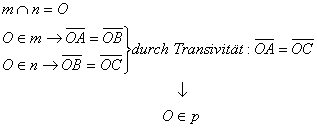
da die Mittelsenkrechte p ist die Menge aller Punkte, die gleich weit von A und C entfernt sind.

Somit ist O gemeinsamer Punkt für die drei Mittelsenkrechten des Dreiecks.

Da gilt, ist O der Mittelpunkt eines Kreises, der durch A, B und C geht (Umkreis des Dreiecks). Der Radius des Umkreises ist.

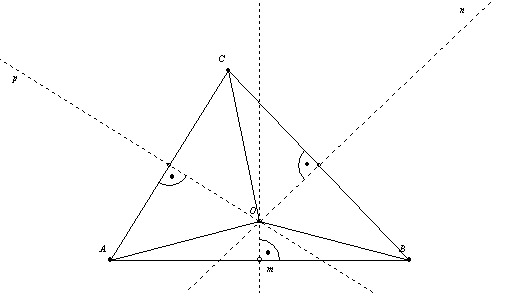
36. Beweisen Sie:

In einem Dreieck schneiden sich die inneren Winkelhalbierenden in einem Punkt, dieser Punkt ist der Mittelpunkt des Inkreises.

Beweis:

Es seien u, v, w die inneren Winkelhalbierenden von ÐBAC,ÐCBA,ÐABC und u Ç w = M

ß

MÎu ® M hat gleiche Abstände von den Geraden AB und AC

MÎw ® M hat gleiche Abstände von den Geraden AB und BC

ß

durch Transivität: M hat von den Geraden AC und BC die gleichen Abstände ® M Î v, da die Winkelhalbierende v ist die Menge aller Punkte, die von den Geraden AC und BC den gleichen Abstand haben.

M ist ein gemeinsamer Punkt der drei inneren Winkelhalbierenden.

Anmerkung:

Wegen der gleichen Abstände (r) zu den Seiten, ist M Mittelpunkt eines Kreises, der die Dreiecksseiten von innen berührt (der Inkreis).

37. Höhen eines Dreiecks

Satz: In einem Dreieck schneiden sich die Höhen in einem Punkt. Diesen Punkt nennt man Höhenschnittpunkt.

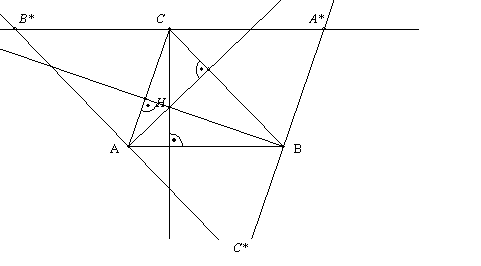
Beweis:

Durch die Eckpunkte des Dreiecks werden Parallele zu den gegenüberliegenden Seiten gezeichnet. So entsteht ein Dreieck A*B*C*.

ABA*C ist ein Parallelogramm: AB = A*C

ABCB* ist ein Parallelogramm: AB = CB*

Þ A*C = B*C Þ C ist Mittelpunkt der Seite A*B*

Genauso sind die Eckpunkte des ursprünglichen Dreiecks Mittelpunkte der Seiten des neuen Dreiecks. Die Mittelsenkrechten des Dreiecks A*B*C* sind also gleichzeitig Höhen des Dreiecks ABC. Da sich die Mittelsenkrechten in einem Punkt schneiden, so schneiden sich die Höhen des Dreiecks ABC auch in einem Punkt.

38. Der Satz von Thales

Satz: Die Menge aller Punkte einer Ebene, von denen aus eine gegebene Strecke AB unter einem rechtem Winkel zu sehen ist, ist der Kreis mit dem Durchmesser AB. Die beiden Endpunkte der Strecke AB gehören der Menge nicht dazu.

Beweis:

1. Aus den Punkten des Thales-Kreises sieht man den Durchmesser unter 90°.

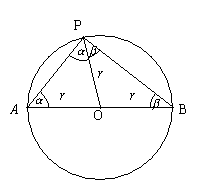Dreieck AOP und Dreieck BOP sind gleichschenklige Dreiecke OA = OP = r bzw. OB = OP = r (Schenkel = r).
Daraus folgt:
ÐOAP = ÐAPO = a ÐBOP = ÐBPO = b

Die Innenwinkelsumme des Dreiecks ist 180°, so ist im :
a + b + ( a + b ) = 180°

2a + 2b = 180°

a + b = 90°

ß

Ð APB= 90°

2. Weder außerhalb noch innerhalb des Kreises gibt es Punkte, von denen aus der Durchmesser unter 90° zu sehen wäre.

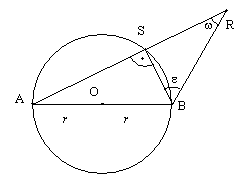a, R liegt außerhalb des Kreises

Man verbindet R mit A, der Schnittpunkt mit der Kreislinie ist S.

ÐASB ist ein Außenwinkel des Dreiecks SBR, gleichzeitig ist er 90° (wegen Beweis1.).

ÐSBR + ÐSRB = ÐASB

e + w = 90° Þ w < 90°

b, Q liegt innerhalb des Kreises

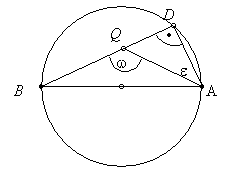
Man verbindet Q mit B, der Schnittpunkt mit der Kreislinie ist D.

ÐAQB ist ein Außenwinkel des Dreiecks ADQ, dessen Winkel ÐADQ 90° beträgt (wegen Beweis 1.).

ÐAQB = ÐDAQ + ÐADQ

w = e + 90° Þ w > 90°

40. Sehnenviereck

Satz: Ein Viereck ist dann und nur dann ein Sehnenviereck, wenn die Summe zweier gegenüberliegender Winkel 180° beträgt.

1. Im Sehnenviereck ist die Summe zweier gegenüberliegender Winkel gleich 180°.

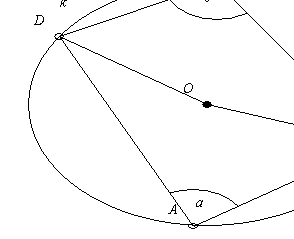
Beweis:

a ist ein Peripheriewinkel über BCD Þ Mittelpunktswinkel: 2a

g ist ein Peripheriewinkel über BAD Þ Mittelpunktswinkel: 2g

Zusammen bilden sie Vollwinkel:

2a + 2g = 360°

a + g = 180°

genauso: b + d = 180°

2. Ist in einem Viereck die Summe der gegenüberliegenden Winkel 180°, so ist das Viereck ein Sehnenviereck.

Beweis:

a, a = g = 90°

BD: Durchmesser des Kreises Þ man kann Thales-Kreis konstruieren Þ A, B, C, D Î k

b, a ¹ g a > 90° g < 90° g = 180° - a (aus der Voraussetzung)

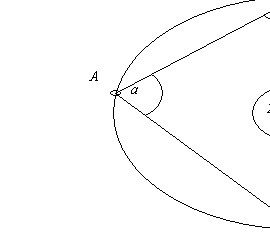
Drei Punkte bestimmen immer einen Kreis (Umkreis von Dreieck ABD) Þ A,B,D liegen also auf einer Kreislinie.

Man muss beweisen, dass C auch auf dieser Kreislinie liegt.

a: ist ein Peripheriewinkel über BD Þ Mittelpunktswinkel ist: 2a Þ Mittelpunktwinkel über BAD ist: 360°-2a Þ alle Peripheriewinkel über BAD sind die Hälfte davon, also:180°-a groß.

Da g auch 180°-a ist (Voraussetzung), so muss der Scheitelpunkt von g auch auf der Kreislinie liegen Þ A, B, C, D liegen auf einem Kreis

42. Die Winkel und die Diagonalen eines Vielecks

Definition: Vieleck nennen wir eine ebene Figur, die durch in der Ebene liegenden Strecken begrenzt wird. Diese Strecken sind die Seiten des Vielecks. Das n-seitige Vieleck hat n Ecken und n Winkel.

Ein Vieleck ist konvex, wenn die Verbindungsstrecke zweier beliebiger Punkte des Vielecks innerhalb des Vielecks verläuft.
Ein Vieleck ist konkav, falls in ihm zwei Punkte existieren, deren Verbindungsstrecke teilweise auch außerhalb des Vielecks verläuft.

Satz: Das n‑seitige konvexe Vieleck hat Diagonalen.

Beweis: Von einer beliebigen Ecke zeichnen wir alle Diagonalen.

Das n-seitigeVieleck hat n-3 Diagonalen, da zu den benachbarten Ecken und zu dem gewählten Punkt selbst keine Diagonale gezeichnet werden kann. Von den Ecken des Vielecks können insgesamt Diagonalen gezeichnet werden, aber so haben wir alle Diagonalen zweimal gezählt (bei beiden Endpunkten), deshalb müssen wir die Anzahl durch 2 teilen: .

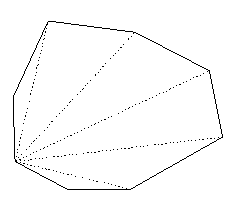
Satz: Die Summe der Innenwinkel des n-seitigen Vielecks ist .

Beweis: In dem n-seitigen Vieleck kann man von allen Ecken n-3 Diagonalen ziehen. Die n-3 Diagonalen zerlegen das Vieleck in n-2 Dreiecke. Die Summe der Innenwinkel eines Dreiecks beträgt 180°, so beträgt die Summe der Innenwinkel des Vielecks .

43. Zusammenhang zwischen dem arithmetischen und geometrischen Mittel zweier Zahlen

a und b sind beliebige nichtnegative Zahlen, deren arithmetisches Mittel ist und deren geometrisches Mittel ist.

Satz: Das geometrische Mittel zweier nichtnegativer Zahlen ist nie größer als das arithmetische Mittel derselben Zahlen. In Formeln:; wobei gilt.

Beweis auf algebraischem Wege:

die Umformung ist äquivalent, da beide Seiten nicht negativ sind

Die letzte Zeile gilt immer, da das Quadrat reeller Zahlen nie negativ wird.

Da diese letzte Zeile gilt und man nur äquivalente Umformungen gemacht hat, stimmt die ursprüngliche Ungleichung auch.

Wenn , dann sind die zwei Mittel gleich.

Beweis auf geometrischem Wege:

a und b sind zwei Strecken, deren Summe der Durchmesser eines Kreises ist.

Wir errichten eine Senkrechte im Treffpunkt der beiden Strecken (H) und im Mittelpunkt des Kreises (O).

Nach dem Satz von Thales ist rechtwinklig, die Strecke ist die Höhe zur Hypotenuse, die laut dem Kathetensatz das geometrische Mittel der Strecken a und b ist (also ).

Die Strecke ist der Radius des Kreises, also ihre Länge ist die Hälfte des Kreisdurchmessers: (also ). Die Strecke ist eine Halbsehne, die kleiner gleich dem Radius ()sein muss. Daraus folgt: .

Wenn dann sind die zwei Strecken gleich, so sind die zwei Mittelwerte auch gleich.

44. Was versteht man unter Kongruenzabbildungen?

Definition: Die Kongruenzabbildungen sind streckentreue geometrische Transformationen. Jede Figur F wird in eine deckungsgleiche (kongruente) Figur F' abgebildet.

Das Bild einer Strecke und die ursprüngliche Strecke sind gleich lang.

Eigenschaften:

Die Kongruenzabbildungen sind geradentreu, winkeltreu und kreistreu.

Beispiele:

- Achsenspiegelungen

- Punktspiegelungen

- Drehungen

- Parallelverschiebungen

- sowie Verkettungen dieser Abbildungen

Zeichen der Kongruenz: (z.B.: )

45. Welche Punktabbildungen der Ebene werden Achsenspiegelungen genannt? Welche Eigenschaften haben die Achsenspiegelungen?

Achsenspiegelung (Spiegelung an einer Geraden):

Gegeben ist eine Gerade s, die Spiegelachse.

Vorschrift: 1. Jeder Achsenpunkt wird auf sich selbst abgebildet. 2. Jedem Punkt P, der nicht auf der Achse liegt, wird ein Bildpunkt P‘ so zugeordnet, dass die Gerade s die Mittelsenkrechte der Strecke ist.

Eigenschaften:

· Diese Abbildung ist geradentreu, längentreu, kreistreu und winkeltreu.

· Fixpunkte sind alle Punkte der Spiegelachse.

· Die Spiegelachse ist eine Fixpunktgerade.

· Fixgeraden sind alle zur Spiegelachse senkrechten Geraden.

Weitere Bemerkungen:

Der Umlaufsinn der Figuren ändert sich.

Gerade und Bildgerade schließen mit der Achse den gleichen Winkel ein,	oder sind parallel zueinander und zu der Achse.

46. Welche Punktabbildungen der Ebene werden Punktspiegelungen genannt? Welche Eigenschaften haben die Punktspiegelungen?

Punktspiegelung (Spiegelung an einem Punkt):

Gegeben ist ein Punkt Z, das Zentrum.

Vorschrift: 1. Das Zentrum wird auf sich abgebildet. 2. Jeder Punkt P () wird so auf einen Bildpunkt P´ abgebildet, dass das Zentrum Z der Mittelpunkt der Strecke wird.

Eigenschaften:

Diese Abbildung ist geradentreu, längentreu, kreistreu und winkeltreu.

Das Zentrum ist der einzige Fixpunkt.

Weitere Bemerkungen:

Der Umlaufsinn einer Figur bleibt unverändert.

: Gerade und Bildgerade sind parallel zueinander.

: Gerade und Bildgerade fallen zusammen.

47. Was versteht man unter achsensymmetrischen und punktsymmetrischen Figuren? Nennen Sie Dreiecke, Vierecke und Vielecke, die achsen- bzw. punktsymmetrisch sind!

Definition: Achsensymmetrische Figuren sind Figuren, die durch Achsenspiegelung in sich selbst übergehen.

Beispiele:

- das gleichschenklige Dreieck	1 Symmetrieachse
- das gleichseitige Dreieck	3 Symmetrieachsen
- das symmetrische Trapez	1 Symmetrieachse
- das Drachenviereck	1 Symmetrieachse
- der Rhombus	2 Symmetrieachsen
- das Rechteck	2 Symmetrieachsen
- das Quadrat	4 Symmetrieachsen
- alle regelmäßigen n-Ecke	n Symmetrieachsen

Definition: Punktsymmetrische Figuren sind Figuren, die durch Punktspiegelung an einem Punkt in sich selbst übergehen.

Beispiele:

- das Parallelogramm und daher auch: Rhombus, Rechteck, Quadrat.

- die regelmäßigen Vielecke mit gerader Seitenzahl

Bemerkung:

Es gibt kein punktsymmetrisches Dreieck.

48. Welche Transformation der Ebene nennen wir Drehung um einen Punkt? Zählen Sie ihre Eigenschaften auf!

Drehung:

Gegeben ist ein Punkt Z, das Zentrum, ein Winkel und eine Drehrichtung.

Vorschrift:

1. Das Zentrum wird auf sich abgebildet.

2. Jeder Punkt P () wird so auf einen Bildpunkt P´ abgebildet, dass gilt: und P wird mit der gegebenen Richtung in P´ überführt.

Eigenschaften:

- Diese Abbildung ist streckentreu, winkeltreu, kreistreu, geradentreu.

- Es gibt einen Fixpunkt: das Zentrum Z.

-

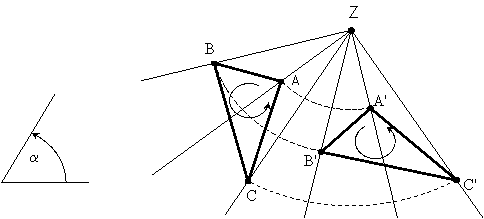
Fixgerade: Die Geraden, die durch Z verlaufen sind Fixgeraden. ().

- Der Umlaufsinn einer Figur bleibt unverändert.

Bemerkungen:

Wenn oder , dann handelt es sich um Identität: alle Punkte der Ebene sind Fixpunkte.

Wenn , dann handelt es sich um eine Punktspiegelung.

49. Welche Transformation nennt man Verschiebung? Zählen Sie die Eigenschaften auf!

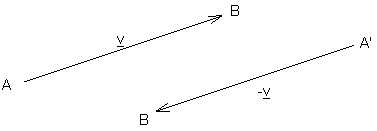
Parallelverschiebung:

Gegeben ist ein Verschiebungsvektor

Vorschrift: Jeder Punkt P wird so auf P´ abgebildet, dass der Pfeil ein Repräsentant des Vektors ist.

Eigenschaften:

- streckentreu

- winkeltreu

- geradentreu

- behält den Umlaufsinn bei

- hat keinen Fixpunkt

Das Bild einer Gerade ist:

Wenn die Gerade und der Verschiebungsvektor nicht parallel sind, dann .

Wenn die Gerade parallel zu dem Verschiebungsvektor ist, dann .

51. Welche Transformation nennen wir zentrale Ähnlichkeitsabbildung? Zählen Sie die Eigenschaften auf!

Zentrische Streckung (Vergrößerung, Verkleinerung):

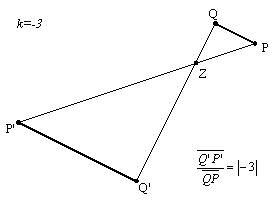
Gegeben sind ein Punkt Z, das Zentrum, und eine reelle Zahl k, der Streckungsfaktor.

Vorschrift: 1. Das Zentrum wird auf sich abgebildet. 2. Jeder Punkt P ( P ¹ Z ) wird so auf einen Bildpunkt P´ abgebildet, dass gilt.
> 1 à Vergrößerung	k = 1 à Identität
< 1 à Verkleinerung	k = -1 à Punktspiegelung

Eigenschaften:

- diese Abbildung ist streckenverhältnisstreu:

- ferner ist die Abbildung geradentreu, kreistreu und winkeltreu

- der einzige Fixpunkt ist das Zentrum der Abbildung

- das Bild einer Geraden ist eine zu ihr parallele Gerade die Bildstrecke ist immer parallel zu der ursprünglichen Strecke.

- geht die Gerade durch das Zentrum, dann ist ihr Bild die Gerade selbst.

52. Was nennt man Vektor? Wann sind zwei Vektoren gleich?

Definition:

Gerichtete Strecken werden Vektoren genannt.

A: Anfangspunkt (Fuß)

B: Endpunkt (Spitze)

Die Länge des Vektors heißt der Betrag des Vektors.

Ein Vektor wird durch seinen Betrag, seine Richtung und Richtungssinn festgelegt.

Zwei Vektoren werden als gleich betrachtet, wenn sie in ihrem Betrag übereinstimmen, parallel sind und den gleichen Richtungssinn haben.

Bemerkungen:

• Stimmen zwei Vektoren in Betrag überein, sind sie parallel und haben entgegengesetzten Richtungssinn, so nennt man sie entgegengesetzte Vektoren. (Gegenvektoren)

• Ist der Betrag eines Vektors 0, so heißt er Nullvektor, sein Zeichnen ist 0.
  Richtung und Richtungssinn eines Nullvektors ist beliebig:

- der Nullvektor ist parallel zu allen Vektoren

- der Nullvektor steht senkrecht auf allen Vektoren

53. Wie definieren wir die Summe, bzw. die Differenz zweier Vektoren? Zählen sie die Eigenschaften der Vektoraddition auf!

1. 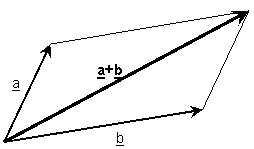VVektoraddition

• Parallelogramm-Methode: die zwei Vektoren werden von einem gemeinsamen Anfangspunkt gezeichnet, dann zu einem Parallelogramm ergänzt; die Diagonale des Parallelogramms ist die Summe der beiden Vektoren.

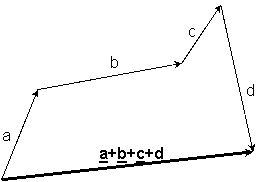
· Methode der sich anschließenden Vektoren: die Vektoren nimmt man nacheinander auf; die Summe der Vektoren ist der Vektor von dem ersten Fußpunkt zu der letzten Spitze.

Eigenschaften der Vektoraddition:

- Kommutativ:

- Assoziativ:

- Es gilt für die Beträge die Dreiecksungleichung:

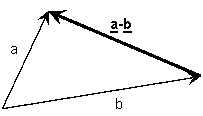
2. Differenz zweier Vektoren

Die zwei Vektoren werden von einem gemeinsamen Anfangspunkt gezeichnet, dann verbindet man die Spitzen der Vektoren. Die Spitze des Differenzvektors zeigt zu dem Vektor hin, wovon subtrahiert wird.

54. Was verstehen wir unter dem Produkt eines Vektors mit einer Zahl?

Multiplikation eines Vektors mit einer Zahl:

Gegeben sind der Vektor a und eine reelle Zahl. Für den Vektor gilt:

1.

2. und a haben

a) die gleiche Richtung, wenn

b) die entgegengesetzte Richtung, wenn

c) ist der Nullvektor, wenn

Eigenschaften:

Für die Multiplikation von Vektoren mit Zahlen gilt: (l, m Î R)

l a = a l (Kommutativgesetz)

l (ma) =(l m) a (Assoziativgesetz)

l (a + b) = l a + l b (Distributivgesetz)

(l + m) a =l a +m a (Distributivgesetz)

55. Beweisen Sie: In einem Dreieck schneiden sich die Seitenhalbierenden in einem Punkt.

Satz: Die Seitenhalbierenden eines Dreiecks schneiden sich in einem Punkt. Diesen Punkt nennt man Schwerpunkt. Der Schwerpunkt teilt jede Seitenhalbierende im Verhältnis 1:2.

Beweis:

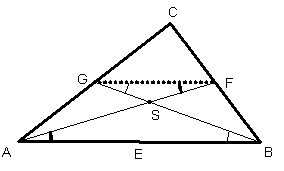
Die Seitenhalbierenden und schneiden sich in einem Punkt: S

ist eine Mittellinie des Dreiecks, daher ist sie parallel zu
und (Wechselwinkel)

So sind die Dreiecke und ähnlich. (Ihre Winkel stimmen überein)

Für die Seitenverhältnisse gilt: , da eine Mittellinie ist.

Wir müssen noch untersuchen, ob die dritte Seitenhalbierende auch durch S verläuft.

Nehmen wir an, dass die Seitenhalbierende die Gerade im Punkt K schneidet.

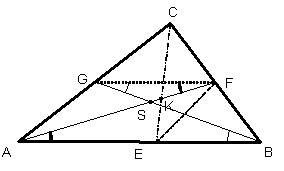
Genauso wie vorher können wir beweisen, dass, da eine Mittellinie ist.

die Punkte S und K fallen zusammen.

Die Seitenhalbierende verläuft also auch durch den Punkt S. So schneiden sich alle Seitenhalbierenden in einem Punkt.

56. Satz von Pythagoras

Satz: In einem rechtwinkligen Dreieck ist die Quadratsumme der Katheten gleich dem Quadrat der Hypotenuse.

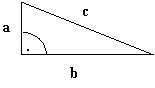
Beweis: Wir betrachten 2 kongruente Quadrate mit der Seitenlänge a + b. Diese werden in Teilfiguren aufgeteilt:

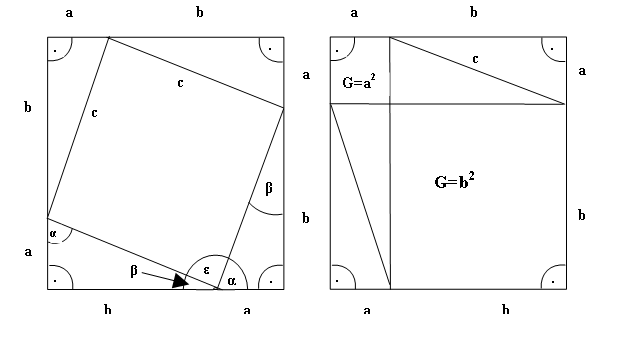
1. Vier Dreiecke + ein Viereck

Das Viereck ist ein Quadrat, da alle Seiten gleich sind:c und ε = 90^o, da α + β = 90^o

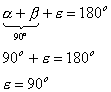
So ist der Flächeninhalt des Vierecks c².

2. Vier Dreiecke + zwei Quadrate mit dem Flächeninhalt a² bzw. b².

Alle Dreiecke sind kongruent, denn sie stimmen in den Seitenlängen a, b und dem von diesen Seiten eingeschlossenen Winkel (90^o) überein.

Von gleichen Flächen nehmen wir gleiche Flächen (4 kongruente Dreiecke) weg, so sind die übriggebliebenen Flächen auch gleich.

Kehrsatz: Ist in einem Dreieck die Quadratsumme zweier Seiten gleich dem Quadrat der dritten Seite, so ist das Dreieck rechtwinklig.

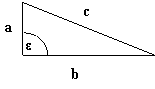
Beweis:

Voraussetzung:

Wir zeichnen ein rechtwinkliges Dreieck mit den Katheten a und b, und bezeichnen die Hypotenuse mit d.

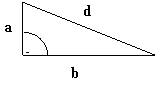
Dann gilt nach dem direkten Satz von Phytagoras: Aus unserer Voraussetzung:

a^2 + b^2 = d^2 a^2 + b^2 = c^2

d^2 = c^2 d= c

Die beiden Dreiecke stimmen in allen drei Seiten überein, also sie sind kongruent, deshalb stimmen die entsprechenden Winkel überein.

57. Formulieren Sie den Strahlensatz und die Umkehrung des Strahlensatzes!

Strahlensatz:Werden die Schenkel eines Winkels von Parallelen geschnitten, so verhalten sich die Abschnitte auf dem einen Schenkel, wie die entsprechenden Abschnitte auf dem anderen Schenkel.

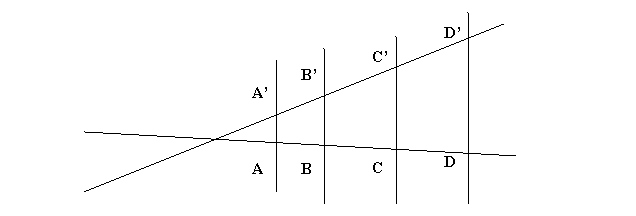
Die Umkehrung des Satzes stimmt im Allgemeinen nicht. Wenn man aber die Strecken von dem Scheitelpunkt aus nimmt, kann man einen Umkehrsatz formulieren:

Umkehrung: Werden die Schenkel eines Winkels von 2 Geraden so geschnitten, dass die Abschnitte auf beiden Schenkeln in demselben Verhältnis stehen, so sind diese Geraden parallel zueinander.

59. Wann nennen wir zwei Figuren ähnlich?

Zwei Figuren sind ähnlich, wenn es eine solche Ähnlichkeitsabbildung gibt, die die eine Figur in die andere überträgt.

Wann sind zwei Dreiecke ähnlich?

1. Zwei Dreiecke sind ähnlich, wenn sie im Verhältnis der Längen entsprechender Seiten übereinstimmen.

2.
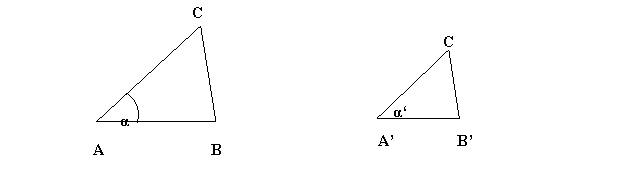
Zwei Dreiecke sind ähnlich, wenn sie im Verhältnis der Längen zweier Seiten und im Mass des eingeschlossenen Winkels übereinstimmen.

; und a = a^,

3. 2 Dreiecke sind ähnlich, wenn sie im Verhältnis der Längen zweier Seiten und im Mass des Gegenwinkels der grösseren der beiden Seiten übereinstimmen.

; und g = g‘ , >

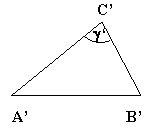
4. 2 Dreiecke sind ähnlich, wenn sie in den Maßen von zwei Winkeln übereinstimmen.

a = a’

b = b’

60. Drücken Sie den Flächeninhalt des Kreissektors und des Kreissegments durch den Radius und den Mittelpunktswinkel aus!

Kreissektor: Der Mittelpunktswinkel verhält sich zum Vollwinkel, wie der Flächeninhalt des Kreissektors zum Flächeninhalt des ganzen Kreises.

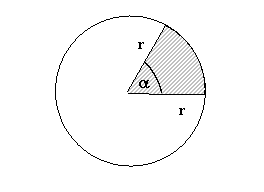
360^o = 2p rad „entspricht“

mit der Bogenlänge: (nach der Definition von Bogenmaß)

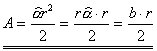
Kreissegment: Flächeninhalt des Kreissegments wird so berechnet, dass man von dem

Flächeninhalt des entsprechenden Kreissektors den Flächeninhalt des Dreiecks subtrahiert.

a in Bogenmaß:

a in^o:

61. Nehmen wir zwei ähnliche Vielecke, bzw. ähnliche Pyramiden, der Ähnlichkeitsfaktor ist in beiden Fällen k. Beweisen Sie, dass das Flächeninhaltsverhältnis von den zwei Vielecken k² ist, das Volumenverhältnis von den zwei Pyramiden k³ ist.

1. Flächenverhältnis ähnlicher Figuren:

a. Nehmen wir zwei ähnliche Dreiecke:

Die Ähnlichkeit ist verhältnistreu, so gilt:

; (*)

; (**)

Die Flächeninhalte der Dreiecke:

Jetzt verwenden wir (*) und (**):

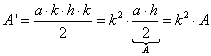
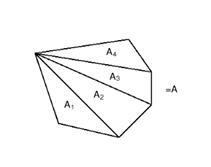
b. Nehmen wir zwei ähnliche Vielecke:

Man kann alle Vielecke in Dreiecke zerlegen.

↑

2.

Volumenverhältnis von zwei ähnlichen Pyramiden:

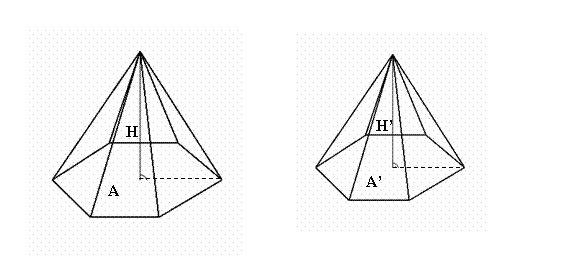
Die Grundflächen sind ähnlich, so gilt:

(Punkt 1.)

Die Höhen verhalten sich folgendermaßen:

62. Welcher Zusammenhang besteht zwischen dem Flächeninhalt der Grundfläche einer Pyramide und dem einer zur Grundfläche parallelen Schnittfläche?

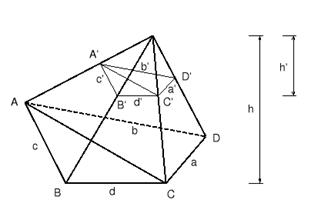Satz: Die Schnittfläche verhält sich zur Grundfläche, wie die Quadrate der Abstände dieser Flächen von der Spitze der Pyramide:

Beweis:

· Da der Schnitt parallel zur Grundfläche ist, liegt eine Ähnlichkeitsabbildung vor, das Zentrum ist die Spitze der Pyramide.

· Der Ähnlichkeitsfaktor ist k.

· Dann gilt für die einzelnen Seiten auch

· .

· In demselben Verhältnis stehen die Höhen der Pyramiden, also: (*).

Wir wissen, dass das Flächeninhaltsverhältnis ähnlicher Figuren gleich dem Quadrat des Ähnlichkeitsfaktors ist (Satz 61.)

63. Beweisen Sie, dass die Kathete eines rechtwinkligen Dreiecks gleich dem geometrischen Mittel aus der Hypotenuse und dem entsprechenden Hypotenusenabschnitt ist.

In Formeln :

Beweis :

Die Dreiecke ∆ABC und ∆ACT sind ähnlich, weil sie beide rechtwinklig sind, und in dem Winkel CAT übereinstimmen. Dann sind ihre Seiten verhältnisgleich :

Genauso folgt aus der Ähnlichkeit von ∆ABC und ∆BCT

(rechtwinklige Dreiecke und CBA ist gemeinsamer Winkel):

64. Zu der Hypotenuse gehörende Höhe eines rechtwinkligen Dreiecks teilt die Hypotenuse in zwei Hypotenusenabschnitte. Beweisen Sie, dass die zur Hypotenuse gehörende Höhe gleich dem geometrischen Mittel aus den zwei Hypotenusenabschnitten ist.

In Formeln :

Beweis:

Die Dreiecke ΔACT und ΔBCT sind ähnlich, weil sie rechtwinklige Dreiecke sind und noch einen gleichen Winkel haben : CAT = BCT = α (da α+β=90°gilt).

Dann sind ihre Seiten verhältnisgleich :

65. Satz über die Tangenten- und Sekantenabschnitte am Kreis

Sekanten-Tangenten-Satz:

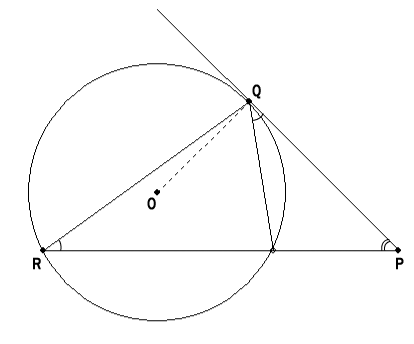
Von einem Punkt außerhalb des Kreises wird an den Kreis eine Tangente und eine Sekante gezeichnet. Der Tangentenabschnitt ist das geometrische Mittel der beiden Sekantenabschnitte.

Beweis:

Wir verbinden den Punkt Q mit den Punkten R und S. Das Dreieck QRP ist ähnlich zu dem Dreieck QSP, weil sie in zwei Winkeln übereinstimmen:

• Sie haben einen gemeinsamen Winkel: ÐQPR = ÐQPS ]
• Der ÐQRP und der ÐSQP sind auch gleich, weil sie zum Bogen QS gehörende Peripheriewinkel sind (ÐSQP mit Tangentenschenkel).

Da die zwei Dreiecke ähnlich sind, sind die Verhältnisse der entsprechenden Seiten auch gleich.

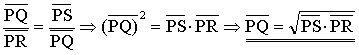
S

66. Wie definiert man die Winkelfunktionen für spitzen Winkel?

Alle rechtwinklige Dreiecke mit dem Winkel a sind ähnlich. So sind die Verhältnisse der Seitenlängen für a auch charakteristisch.

Im rechtwinkligen Dreieck nennt man das Verhältnis der dem spitzen Winkel a gegenüberliegenden Kathete zur Hypotenuse den Sinus des Winkels a.

Ähnlich definiert man die übrigen Winkelfunktionen: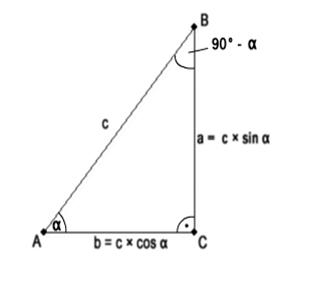

Wichtige Zusammenhänge:

a) sin a = cos(90°- a)

Der Sinus eines Winkels ist gleich dem Kosinus seines Komplementärwinkels.

b) tg a = ctg(90°-a)

Der Tangens eines Winkels ist gleich dem Kotangens seines Komplementärwinkels.

c) sin² a + cos² a = 1

d) , da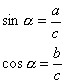

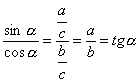
e)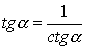

67. Wie definiert man allgemein den Sinus bzw. den Kosinus eines beliebigen Winkels?

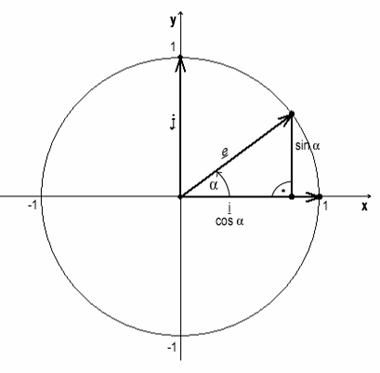r = Radius des Einheitskreises

r = 1

e = Einheitsvektor (Länge ist 1)

α = Drehwinkel

Der Sinus eines beliebigen Winkels α ist die zweite Koordinate eines Einheitsvektors, der um α gedreht ist.

Der Kosinus eines beliebigen Winkels α ist die erste Koordinate eines Einheitsvektors, der um α gedreht ist.

e = cos α i + sin α j

e(cos α ; sin α)

Jeder Winkel hat einen Sinus- und Kosinuswert.

Sinuswerte:	Kosinuswerte:	Die Periode ist 360°, in Radiant: 2π sin α = sin(α + k ^.360°) k Є Z cos α = cos(α + k ^.360°) k Є Z

-1 ≤ sin α ≤ 1

-1 ≤ cos α ≤ 1

68. Wie definiert man allgemein den Tangens bzw. den Kotangens eines beliebigen Winkels?

Definition:

Der Tangens eines beliebigen Winkels a ist der Quotient aus dem Sinus und aus dem Kosinus dieses Winkels, falls dieser Quotient existiert.

Definition:

Der Kotangens eines beliebigen Winkels a ist der Quotient aus dem Kosinus und aus dem Sinus dieses Winkels, falls der Quotient existiert.

Nicht jeder Winkel hat einen Tangens- oder Kotangenswert.

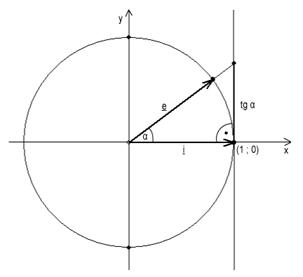
tg 90° und tg 270° …sind nicht definiert Die Periode ist 180°, in Bogenmaß: π. tg α = tg(α + k180°) , k Є Z tg(-α) = -tg α

ctg 0°, ctg 180°, ctg 360°…sind nicht definiert Die Periode ist 180°, in Bogenmaß: π. ctg α = ctg(α + k180°) , k Є Z ctg(-α) = -ctg α

Tangenswerte	Kotangenswerte

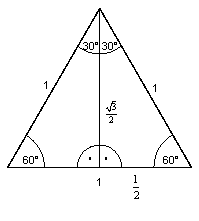
69. Bestimmen Sie die genauen Werte der Winkelfunktionen für die Winkel von 30°, 45°, 60°.

Aus einem regelmäßigen Dreieck (mit der Seitenlänge 1) bzw. einem gleichschenklig-rechtwinkligen Dreieck (mit der Kathetenlänge 1) kann man die genauen Werte dieser Winkelfunktionen bestimmen.

Abkürzungen: GK: Gegenkathete, AK: Ankathete, H: Hypotenuse

Zusammengefasst:

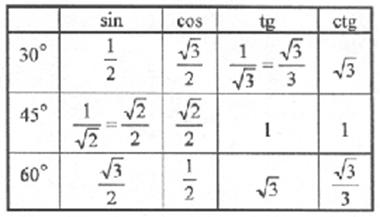
70. Beweisen Sie die folgende Identität: sin²a + cos²a = 1; a R!

Beweis:

Hat ein Vektor v die Koordinaten x und y, ist seine Länge: |v| = |v| ² = x ² + y ²

Ist v der Einheitsvektor, der mit der x-Achse den Winkel a einschliesst, so ist |v| = 1.

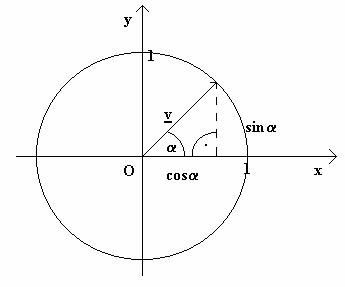
Nach der Definition der Winkelfunktionen sind: x = sina, y = cosa

Damit folgt: sin²a+cos²a = 1

71. Bestimmen Sie den Flächeninhalt des Dreiecks, wenn zwei Seiten und der von ihnen eingeschlossene Winkel gegeben sind!

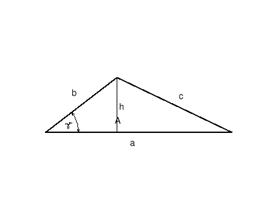
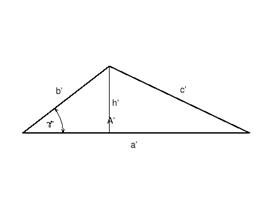
Es ist zu beweisen: A =

Beweis:

a.)

wenn c < 90°

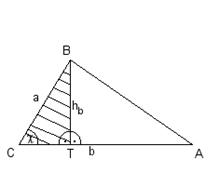
A =

DCTB ist rechtwinklig:

sinc =

a × sinc = h_b

eingesetzt für h_b in die Flächeninhaltsformel

A =

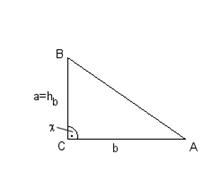
b.) wenn c = 90°

DBCA ist rechtwinklig:

A = ; da a = h _b

A =

A =

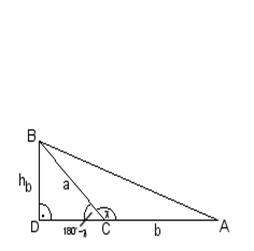
c.) wenn c > 90°

Wenn es ein stumpfwinkliges Dreieck ist, so muss man im DBCD mit h_b = a × sin(180°-c) rechnen:

A =

Aber da sin(180°-c) = sinc :

A =

Zusammenfassung:

für jedes Dreieck gilt:

73. Beweise den folgenden Zusammenhang zwischen der Kreissehne der Länge a, dem Radius des Kreises r und dem Peripheriewinkel a, der zu a gehört: a = 2r × sina.

Beweis:

a, a < 90°

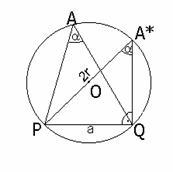
Man zeichnet den Durchmesser , so bekommt man das Dreieck PQA*.

Wegen des Satzes über die Peripheriewinkel ist der Winkel PA*Q auch a, gleichzeitig ist das Dreieck PQA* rechtwinklig wegen des Thales-Satzes, da PA* Durchmesser des Kreises ist.

In dem rechtwinkligen Dreieck gilt:

sina = a = 2r × sina

b, a = 90°

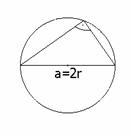
Wenn a = 90°, so ist a = 2r (Thales Kreis)

Auch diesmal ist es so:

a = 2r = 2r × 1 =2r sin90° = 2r × sina

c, a > 90°

Wenn der Winkel a stumpf ist, so muss man das Dreieck PQA* nehmen:

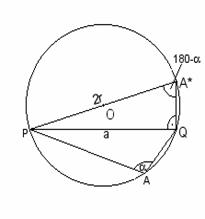
Winkel PQA* = 90°, da PA* Durchmesser ist

Winkel PA*Q = 180°-a, da PAQA* ein Sehnenviereck ist.

So im Dreieck PQA*:

sin(180°-a) = a = 2rsin(180°-a)

Aber da sin(180°-a) = sina ist a = 2r × sina